You need something for the internal edges too. Simplest would be Length goals with restlength of 0.
Smooth instead of Line seems to help but not if I subdivide the mesh…

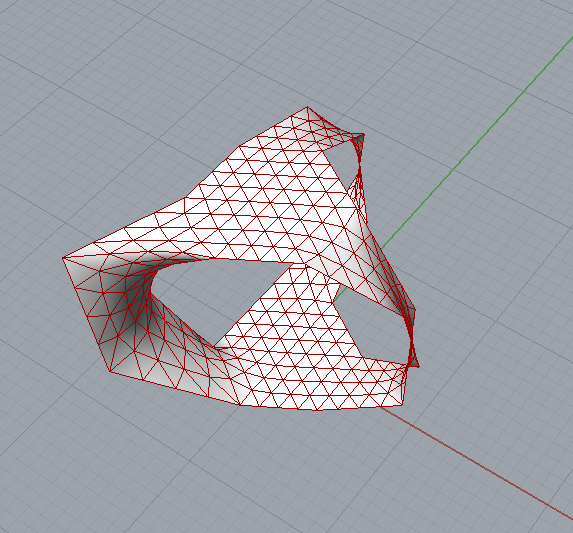
Starting Mesh…

If I subdivide the initial mesh more…
this happens…

trefoil_relax.gh (22.0 KB)
Here’s how I approached this. I was separating the generation of the curve from the mesh relaxation.
It is possible to do them both together, but then the forces keeping the knot curve smooth/repelled from itself need to be strong enough to resist the pulling in of the surface. I’d do this with Length goals and perhaps some bending too.
Oh also, I included a little bonus in that last definition 
Because the trefoil curve is swept out by a 4d rotation, you can apply that same 4d rotation to the surface, and it inverts while staying on the same boundary

Play with the slider to see this transformation
Any chance of a screen shot of the definition so I can fill in the gaps when opening in R5 please?
Could you try something for me if possible… I noticed that relaxing the Trefoil from 2 different starting meshes in Seifert View gave different results…
gives a result similar to yours above…
but using the flat starting mesh…
gives this…
Which looks like the inspiration for the Nat Friedman sculpture but with the knot in the edge.
Any idea why they would relax differently?
I think SeifertView uses the same knot energy function as Scharein does in KnotPlot.
There are some knot energies defined which are Möbius invariant, meaning that Möbius transformations do knot change the energy.
I don’t know if the energy they use is Möbius invariant, but if so, that would explain why it can relax to either.
Both the forms of the trefoil knot you show are torus knots - and can be called (3,2) and (2,3), for the number of times the curve winds around the vertical axis vs the number of times it loops through the hole.
As I illustrated in the animation in the earlier post in this thread though, you can move between them with a Möbius transformation. Here’s an old post from a great topology blog about this equivalence:
…or it could be that even if the energy used is not Möbius invariant, it can get stuck in different local minima, or perhaps one is really an energy saddle point, and with a little perturbation it would switch to the other one.
Here’s a paper by Louis Kauffman on the topic that looks like it goes into just this topic of local vs global energy minima for knots in more detail:
I believe one of the reasons energy minima of knots are studied is that if you can always find your way to the same ‘canonical’ form starting from topologically equivalent but geometrically different curves, you can check if they are the same.
There’s a famous example in Knot theory called the Perko pair, where a table of knots contained 2 drawings that looked different but after many years were discovered to be the same knot.
oh, and here’s the screenshot. I knew you were on R5 so included an internalised copy of the curve so you don’t need the Möbius component
I don’t think there’s anything else there that is different between 5 and 6
(6 has lots of nice improvements though!)
Thanks, I’ll read through all that.
Yeah, I am in desperate need of a new laptop and then an R6 upgrade but that will have to wait.
Just discovered that despite all my efforts, simply running your initial mesh through WBLoop subdivision gives a better result!
Most fun I’ve had on GH for ages though, thanks for all the input.
I mean just subdividing your initial mesh gives a better result than subdividing and relaxing MY efforts 
I created an initial mesh, subdivided it, relaxed it, smoothed it and got somethign almost as good as what you did in one component.
I’m working on it!
This def allows you to change the knot twists but I’m not sure yet how to create the correct edge curve to pull knots with more than 3 twists to.
As it is, it works with 3 but if you select more the torus knot curve needs to match. At the moment I’m trying to find the right combination of P and Q in the torus knot section and then rotating the curve to match the mesh as closely as possible which worked for 3 twists but so far has not worked for more than 3 twists.
Anyone figure out a good way to make the torus knot curve match the mesh automatically?
Ah, it works with 5…
P = 2 (and select neg P)
Q = 5
Rotate Curve 37 degrees.
Hi Daniel,
How do you create the coarse mesh in your “trefoil_relax” definition? Any tips in how to approach creating such topology… I tried a couple of things starting from the trefoil curve but didnt succed (newbie here), whatever I do doesnt results in a smooth mesh after the subdivission. Thanks.
If this approach helps, starting from 4 circles that form a square, 3 surfaces are created and then slightly deformed to obtain an approximation like the one seen.
mesh-trifoil-knot.3dm (215.5 KB)
Last improvement of the shape. I’m thinking about a strategy to join the 2 meshes together…

What do you think?
If the naked mesh edges of your mesh surfaces cleanly intersect each other, you can join your meshes and weld the intersecting vertices. The vanilla Grasshopper components are okay for this, but the Weaverbird one is usually better.
Hi @diff-arch! No unfortunately they are not intersecting well…But thanks for the suggestion! I will try to make some changes so I will be able to use those components!
Looking good!
You might be able to pair up the naked mesh vertices that need to be the same to join the meshes and then pull them together. I suppose it depends how far apart they are to begin with.
I did it with kangaroo! I joined the vertices in the middle so I was able to join both meshes together. The problem is that in this way I create a crease in the joining area and when I smooth the mesh the result is not clean… I will upload the picture of the problem when I go back to work!
So is the approach essentially what @DanielPiker did to create the first surface, then rotate it 180degrees, then join the meshes to create the volume and finally smooth to round the edges?
Can you control that centre section? If you notice on the original image of the sculpture by Nat Friedman the centre has a bit more twist in it than yours. I found it really hard to get this right.