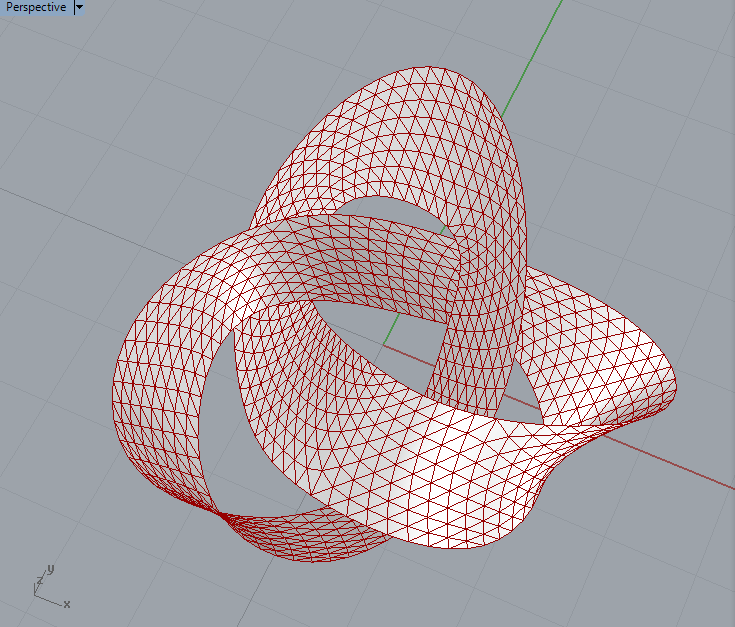
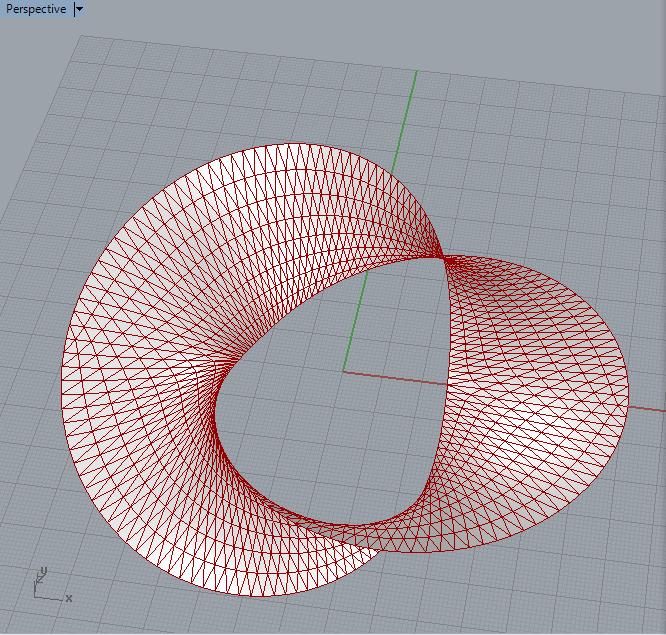
Maybe… it would be interesting to see if Mesh Loft could handle it.
I actually prefer the sharp edge that Daniel created in that last image.
Torus Knots… no volume but fun to play with.
I’m relying on the pFrame component to orient the ribbon surface around the torus knot curve and this might not be correct.
TORUS_KNOT.gh (21.5 KB)
Nice use of ruled surface.
Does anyone know if the ribbon surface is correctly generated? If you look up the different torus knots generated from different p and q combinations this def seems to create the right curve but the surface doesn’t always look right.
Also… Back on topic… Still haven’t managed to get a surface with rotational symmetry that can enclose a volume like Daniel’s solution above.
Yes I understood I just wanted to see if I was able first to get also your first result with the real minimal surface!
Working now on the original shape from the image… I will show you what I can get
To my eye (former gem carver, many years) it appears as Daniel has said, 2 surfaces enclosing a volume. Probably was carved using the two surfaces as the final goal, with a sharp edge, then sharp edge blended between each surface as last step. From the photo, appears to be a phenomenal carving job, great execution with no visible mistakes in an unforgiving design in an unforgiving medium.
When I try the 2 surfaces way of creating this I get stuck trying to get the vertices on the edges to match up so they can be welded and further smoothed…
(Pretty horrific Loop subdivision rather than MeshMachine or K2.)…

Edges here don’t quite line up.

Anyone any tips on strategy to create each surface so they match up when rotated? Pull points together or plan for rotational symmetry?
My starting surface topology is pretty poor too but I don’t understand how you could start with a simple topology and end up with matching vertices after remeshing etc.
Sort of there now but it still lacks that something that makes it a great shape like the original sculpture…
Some weird things happen in this definition too…
-
The 2 surfaces only seem to nest together properly if sliders DIVIDE COUNT 1 & 2 are set to 5 and 6 respectively.
-
If I weld the final mesh I get a closed mesh when I bake it to Rhino but the edge gets effected by the Weld operation - WB Weld flips the mesh faces and the other 2 Weld components don’t flip the faces but effect the edge slightly.
-
I have no idea what I’m doing with MeshMachine… basically infinite monkey approach until something works.
-
There is nothing minimal about these surfaces as far as I can tell.
-
There is nothing Trefoil Knot related either!
Perhaps I’ll try and machine one and then sand it for about 4 years!
THING_2.gh (28.4 KB)
Depends on what you are machining it out of, I guess (:
Oak.
I would love to have a .3dm of that shape.
It plays your mind very nicely.
Paul Fuchs
I’m not sure this adds anything to this discussion, but here it is anyway:
This is a modified version of Marty’s file - I took out some stuff at the end because I was just using the edge curves, and I put in a Scale factor because my default dimensions are millimeters.
I suspect there are better ways of using the WB components to make a smoother final shape.
TORUS_KNOT-bb1.gh (27.2 KB)
I tried to build the shape by using the @DanielPiker approach but I can not get a result that I’m happy with… I tried to replicate the same original mesh you did in the picture but I can’t get a nice shape as you did. I have the same problems that @martynjhogg has about joining the 2 surfaces together and also the problem to make them match. Said that for me the algorithm @martynjhoggused for me has more sense because start from a shape that it could be a simplification of the final result. The problem is that it’s not a perfect circle. So I don’t know how to solve it 
It’s driving me crazy too!
Makes you appreciate the original sculpture even more.
The design just doesn’t work without that mathematical perfection.
Or is it just an amazing sculptor carving something by eye that is inspired by minimal surfaces and trefoil knots?
It feels like we’re missing an important step that controls the shape to give it that perfect symetry and form.
Hmm. One of the cliches for sculpting is taking away everything that doe not need to be there. It took several years for this to click for me, but it is true, you are removing the material that does not need to be there.
Observing the original artwork, I see the date of the photograph is 2006. So the piece was probably started, perhaps as a study piece, in 2002 or 2003. And he probably worked on it, on and off, for perhaps 400 hours over 9 months or so.
So, the year is 2003. How would you start doing this?
I think the key is in your observation of ‘mathematical precision’. Sadly we did not have grasshopper in 2003. I am thinking it is worth looking at a strict mathematical approach to the shape using mathematical equations, one set for the form itself, and another to add thickness.
At about the same time (2005-7) I did a series of carved nephrite jade pieces using that approach, equations hardcoded in, of all things, “pure basic”. And it worked! much to my surprise
Do sculptors hate 3d printing then?
Definitely not all of them!
Take a look at the work of Bathsheba Grossman and Rinus Roelofs for just 2 examples, both sculptors, and both long time users of Rhino and 3d printing. Grossman in particular I think was an early pioneer of 3d printed sculpture, long before such easy mail order services as Shapeways existed.

Borromean Rings Seifert Surface, Bathsheba Grossman
Connected Holes - Rhombic Dodecahedron, Rinus Roelofs
I do find it fascinating in the world of fine art sculpture the interface of intuitive and hand crafted work with digital processes. Particularly where the resulting forms are (at least apparently) highly mathematical rather than figurative.
Another 2 sculptors whose work I admire are Carlo Séquin and Eva Hild. Their work deals with similar themes of smooth hyperbolic and minimal surfaces and topological complexity, but their approaches are in some ways at opposite extremes.
Séquin is a professor of Computer Science, and a long time researcher and developer of computational methods for geometric design, and many of his sculptural works are 3d printed, and they often have associated publications describing the algorithms used.

Pentagonal Dyck Cycle, Carlo Séquin
Hild on the other hand doesn’t involve computers or equations in her work at all from what I’ve read, and she arrives at these forms through a direct and tactile process. Perhaps what many would see as a more fine art approach, yet the shapes look very much like the outcome of an energy minimising process, and people often think they are mathematical or computationally generated.
Ceramic Sculpture, Eva Hild
In between I think there is a great range of sculptors who use some level of mathematical and computational techniques, but where the work is not necessarily a ‘pure’ result of one algorithm, or completely fabricated by CNC milling or 3d printing.
Another of my favourites is Robert Longhurst, who works by hand, but shows a strong mathematical influence.
Arabesque XLII, Robert Longhurst