Construct a polyarc like structure with constraints

[Ramina]

Hi Grasshopper community!

I am working in one architecture atelier as programmer and I got an assignment in Grasshopper. Never worked there before and need some community help.

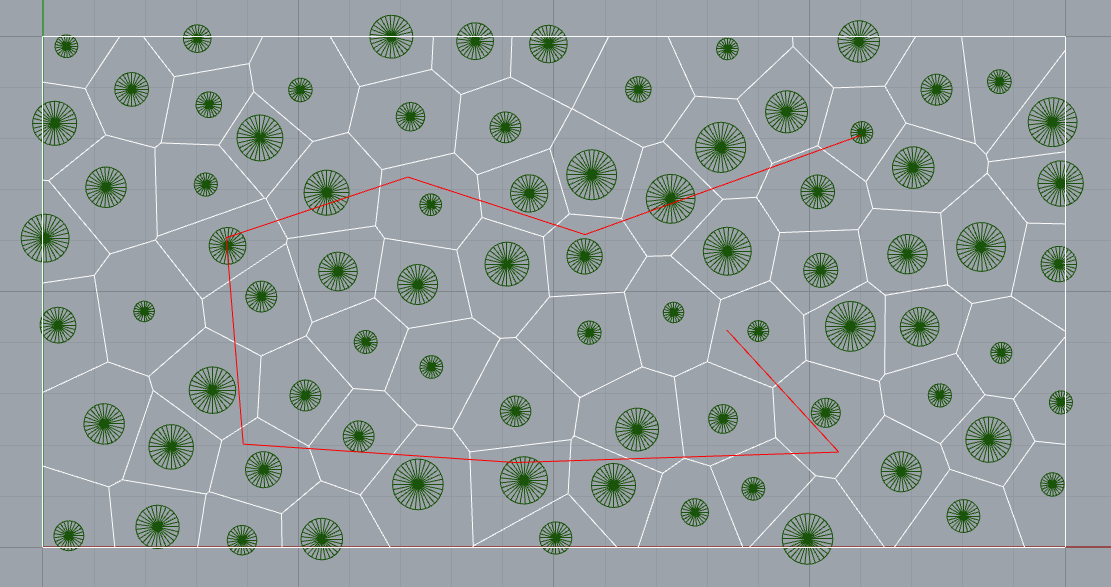
I have a csv file with trees coordinates in a park (x, y, safe_radius). I have it visualized as points and circles around them.

Then, I define a list of points in the viewport. The first is supposed to be the start, the last - end of the curved wall. In between points are suppose to mark the approximate direction of the wall. The goal is to construct a curved wall, so that it does not intersect any safe area of any tree and has some more constraints:

• Wall consists of segments of length SEG_LEN (1m<=SEG_LEN<=3m).
• Every segment is an arc of a circle of two predefined radiuses (SEG_RAD_1, SEG_RAD_2).
• Between the segments there should be a gap of a variable length (SEG_GAP \in <2mm, 10mm>).
• Wall must not intersect the tree safe zone (or very slightly).
• It should be smooth

It is a bit overwhelming for a first task and I have no idea how to address this problem. I was thinking about implementing some king of constraint satisfaction optimization algorithm, but it seems a bit overkill. Maybe there are some built-in functions to use for this task I’m not aware of. Couldn’t find any related topics/tutorials/blogs so asking here now.

Any ideas? Would be really grateful for your help.

[Joseph_Oster]

@Ramina

It is a bit overwhelming for a first task

That’s an understatement Looks “advanced” to me. In any case, you need to read this to give people something more to work with than a verbal description and image:

Help Us Help You

Asking questions and getting answers is what this forum is all about. Although people are generally very helpful, there are things you can do to improve your chances of getting good and quick answers. Below you will find some suggestions, but don’t think of them as rules and especially don’t think of them as guarantees. 1. Choose a descriptive title for your post Don’t title your question Help! or I have a problem or Deadline tonight!, but actually describe the problem you are having. 2. Be s…

3. Attach minimal versions of all the relevant files

@Ramina

• Between the segments there should be a gap of a variable length (SEG_GAP \in <2mm, 10mm>).

[inno]

my first thought was that this would be sort of Kangarooable, at least up to a certain degree

then I had this weird vision of solving it using a Voronoi diagram centered on the tree positions -because Voronoi is always the key- but I got taken away by the thing I could actually draw trees as lines pointing from the center of each circle to division points of the circle itself, which looks very cool, and didn’t continue on that path (but very very cool indeed…)

speaking of the matter, it looks to me like a decision tree where each step you can choose direction and length of the next arc based on something like this:

regardless of how you ended up into a given point, the info you have is:
→ the point where you are now (START)
→ the tangent vector of the previous arc, that identifies the position of the centers of your next arcs (in blue)
→ the min/max amount you can walk along arcs A, B, A’, B’

so even if at the end you have to build arcs to move around the final path, maybe an idea would be to pre-calculate the available vectors that move you from start to given points on A, A’, B, B’ and start combining just those in such a way you “keep following” more or less the polyline built over the initial points that define your final path

using GH plugins (like Anemone) and no coding, I don’t know how much deep you might be willing to go with decision making… I’m not a big head but this looks like a case study for recursion with some sort of backtracking in case there are some dead-ends that make you hit a tree regardless of next A, A’, B, B’ ? or maybe it’s just too much gin tonic? is this kangarooable for real? maybe the problem is much easier and this is just an overkill who knows

if you want to give us some numbers, or maybe even better a GH file where the trees are and the points that define the path (and the arcs radii and min/max lengths…) are already there
or maybe those numbers are just generated randomly for the sake of the problem itself? again, who knows

[René_Corella]

@inno

LMAO

[daniMunthali]

clearPath20240127.gh (16.0 KB)
Hi Ramina
I have attached a gh file, with a function that does what you want (to the best of my understanding).
It is a very simple function, so it is not very accurate, but it does the job simply and quickly. However, it does not always work, for example in instances where two tree canopies overlap to create a single volume.