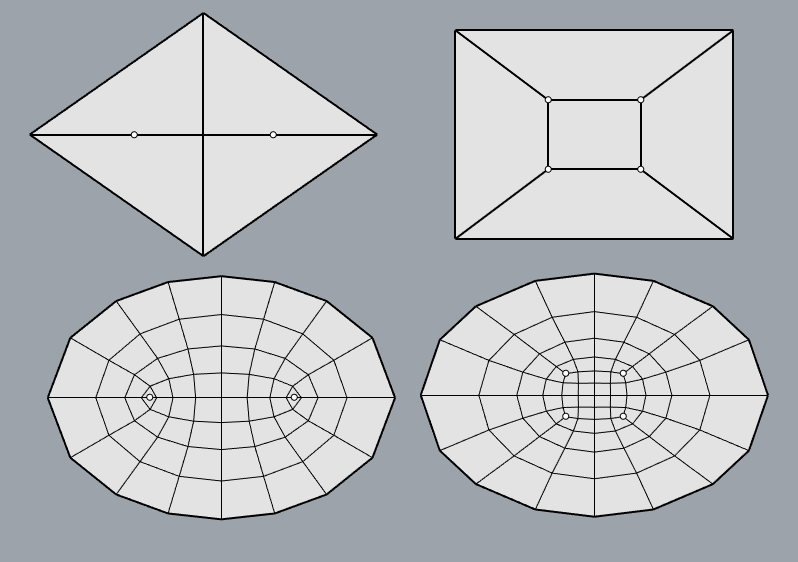
Looks like these two cases strangely haven’t been mentioned yet - the simplest options if you want to match a smooth boundary curve with all quads:
The one on the left is of interest because it can match the principal curvature directions on an ellipsoid-like shape, which is helpful if you intend to make planar panels (see this discussion).
(Principal curvature networks only ever have nodes of even valence)
The layout on the right can be seen as a splitting of each of the valence 2 nodes of the left layout into a pair of valence 3 nodes. While this won’t match smooth curvature directions so well, the variation in panel sizes and angles can be smaller.
For designers I think there’s not really any substitute for developing a feel/understanding for what works and what fits your aesthetic, and creating the patch layout directly yourself. It’s a real art, and when done well can have a great impact on the look of the finished project. I wrote this post a while back about some of the subtleties of the patch layout for the Great Court roof.
One thing to note - if you look at each of the irregular vertices above (the ones not connected to 4 neighbours) and see how many short of 4 surrounding faces it is, and add these values up for all the irregular vertices, the total comes to 4 for any all quad division of a topological disk like this.
(for boundary vertices you have to count how many short of 2 connected faces the irregular vertices are)

Whatever further irregular vertices you add, this total always stays the same. If you have interior vertices surrounded by more than 4 faces (or boundary vertices connected to more than 2) then you have to subtract this value from the total.