Curve Order After Trim

[davidchristiankoch]

Hi,
I am trying to measure the slope of a site and create bands of color showing different slopes. I have contour lines and the site boundary. Essentially, the approach I am taking is to divide each contour line by distance and find the closest point to each of these points on its neighboring contour. I can then measure the distance between these pairs of points to get the slope.

I am using the trim with region component to get the contour lines within the site boundary. This is where I run into a problem because some of the contours snake in and out of the site. This throws off the order of the contours and causes the shift list component to find the wrong neighbor.

I think what I need to do is take the curves that are broken into two or more segments by the trim and reconnect them into one. I haven’t been able to do this despite many hours of effort. If anyone has another solution to this problem I am open to ideas.
CURVE ORDER AFTER TRIM.3dm (98.7 KB)
CURVE ORDER AFTER TRIM.gh (18.1 MB)

[PeterFotiadis (Pfotiad0)]

Well … that’s rather easy via code (components is not my game).

First of all the divisions sould being proportional to a curve length with respact say the min length of all the segments in the parcel (meaning that some var Div should point/refer to the min length curve):

int div = (int) Math.Round(segmentLength/minLength,0) * Div;

Other than that study the screenshot with some abstract demo case on the right in order to get the gist of the bridging logic for your quads (working on pairs of curve segments Lists: say the current one and the next one - these may (or may not) contain more than 1 items). Meaning that depending on the topology per pair you should find what segment in the current List is the master (with regard the divisions) and what is the slave in the next List (with regard the closest points)).

For instance in the top most pair shown and provited that the curves are properly oriented each other (DotProduct and the likes) : the red start should yield a closest point on the green and the green end should yield a closest point on the red etc etc.

Notify if you want a 100% code (C#) based solution on that one

[davidchristiankoch]

Thanks for your reply Peter,

I’m not sure what you mean by divisions being proportional to the length. The method of dividing the curves is less important. I figured I could increase the number of divisions until I got the required resolution.

It looks like you did manage to solve the problem of finding the correct pairs of curves and sharing the code would be a help.

Thanks again!

[PeterFotiadis (Pfotiad0)]

OK, I’ll prepare the demo soon.

See the matching segments concept in more detail (I had this C# already) - spot that the connections are “as uniform as possible” since the min curve length is involved when dividing (bridging) each pair:

But the best way for that is to elevate the curves (since there’s data available for that) , do the divisions and then create a Mesh and then color the faces according some rule (say: how far the face normals deviate from Plane.WorldXY.ZAxis). That said since Delauney is a no-no for similar cases … I can’t post Ball Pivot related Methods (for the Mesh) since these are strictly internal to the practice. Patch … er … hmm … let’s avoid that at any cost (VERY slow).

But … well … if you are after slopes what about a crosshair “help” thingy that could locate a search Point in a given curve (from the ones sampled in the parcel) and then just display (TextDots and the likes) the slope VS the previous/next one? (by getting the closest points and computing the vector angle VS Z).

[PeterFotiadis (Pfotiad0)]

BTW: What has to do the sync Sort here?

Do we have Curves and do we have Elevations and do we assume that are matching 1:1 ?

If so … the whole thingy is rather elementary my dear Watson:

[davidchristiankoch]

You are right that the elevation data is 1:1. I should have shared this earlier but it explains the final output that I need.

There might be a way of using your approach but I’m not sure how you would achieve the discreet bands.

[PeterFotiadis (Pfotiad0)]

That’s very easy (using a custom Class or … rather better clustering doubles [a kind of K-Means, so to speak] derived from the Mesh Faces normal angles [to Z+]).

In any case the sync Sort was out of question (nothing to do with the desired goal and 100000% off topic).

[René_Corella]

Hi David,

Interesting problem - easy for Peter obviously.

Here’s a forced approach as I had something that looked similar - using contouring and some fake ‘parcel’ creation based on some stuff - most likely useless and doesn’t solve your problem but it was fun
CURVE ORDER AFTER TRIM.gh (18.1 MB)

playing with the graph mapper can yield other funkilicious parcels

later

[PeterFotiadis (Pfotiad0)]

Here’s a start point on that matter. Your approach for dividing is completely abandoned for obvious reasons. A mesh approach is used instead where the color part is not yet implemented (that’s rather easy) since 90% of this C# stuff attached was already on hand and I haven’t found time to add the final cut of the mustard.

If we forget the Elapsed time required for the curves VS the boundary part … the big issue here is to use a Method that yields the min possible Elapsed time with regard the mesh creation (coloring is real-time so forget that part). So … patch is out of question (and Ball Pivot is internal): meaning a flat (filtered in boundary) Delauney is used and then another Method does the final elevated mesh (see comments on that below).

Terrain_Slope_V1.3dm (490.7 KB)
Terrain_Slope_V1A.gh (18.2 MB)

That said storing your data (18Mb) in the GH file is VERY RISKY and I would strongly recommend to reference them (Curves) from some R file and used some Excel (Elevations).

That said 280 milliseconds for the mesh (on a slow I5 that is always used for testing performance matters) is not that fast … but 95% of the time is consumed for mapping MTV vertices back to the division points (using a Point3dList) and thus to Z values. Using a proper I9 or a Ryzen time drops to 100 milliseconds max. This is the guilty line:

Division points are proportional to the min length curve (use skip and watch the sorted lengths values to have an idea of what you are doing/using).

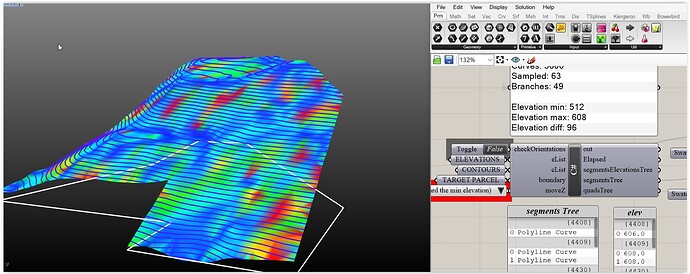
Testing random parcels … rises the need for some intelligence with regard the min curve length (a best pick ability, that is) and/or a better point selection policy for the Delauney by interpolating points to the ones derived from the curve divisions (I’ll add all that in the next update):

More (the final slope/color part) soon: clustering the mesh faces in predefined intervals according the mesh faces normal angle to the global Z.

Update:

Found some minutes for the clustering thing (it’s very simple in fact: you define Intervals according a min/max angle and a partition var [the resolution] and after 10-20 milliseconds the old I5 does the job):

Terrain_Slope_V1B.gh (18.2 MB)

Note: If some faces are not sampled it means that their normal, Z angle is > than the maxAngle. The normal is checked (DotProduct) against the Z so no worries about the mesh orientation.

Note: no elaborated checks are included with regard the data: avoid feeding the thing with bananas.

Note: Filtering Delauney faces inside the boundary is a bit primitive (testing for inclusion of the face center). Done that way for speed. Some times results like this captured occur … but the other way (ccx on topo edges) is quite expensive (but why bother? that’s the 1M question).

[davidchristiankoch]

This is amazing Peter, thanks for your help. After another night working on my approach I’m ready to abandon it. I solved my initial problem but then promptly ran into another one when I tried to create closed regions out of the lines and match them with the slope. I will give this a shot tonight and let you know how it goes.

[PeterFotiadis (Pfotiad0)]

@davidchristiankoch

I’m ready to abandon it.

Adios amigos then: a wise thing to do.

Here’s the trad update (of the update (of the update)): a more trad coloring method (gradient instead of the CW) + a conn tree + a demo Class for any query imaginable (see comments) but for that you’ll need to speak C# + changes here and there for more speed. That said the upgrade: V2 is ready (a major departure from the V1x ways/Methods) but is under testing and ETA is uknown..

Terrain_Slope_V1C.gh (18.2 MB)