Hi there. I am working on a definition that packs random radius (within a range) circles in an enclosed boundary. It works pretty well except that the resultant circles sometimes clip into each other. I have tried fiddling with all of the settings in the ImgCircles component to no avail. Any ideas? Maybe the definition I am working on is the wrong approach. I have tried several other definitions that tackle this problem with varying degrees of success from this very forum. They each have their drawbacks.
Enclosed Boundary Circle Packing.gh (1.1 MB)
1 Like
i honestly never got circle packing to be 100% precise, tried a few definitions. one way could be to use spheres or maybe better cylinders and make dynamic packing, like so i at least managed in another application to get bettter results. one might also be able to do that with kangaroo but never tried. there is also MeshMachine which is within Kangaroo. it lets you do a circle packing but i dont know where a sample definition of that would be, maybe @DanielPiker would be so kind to share one or could comment on an effective method to avoid intersections.
Daniel’s stuff is everywhere I looked. Most of the definitions I tried were made by him. His GitHub has loads of packing examples and I tried them all. I thought about using cylinders as you suggested but I’m unsure how to proceed. Solid collide in Kangaroo2?
Hi Cole,
One thing I notice in that definition is that the points are sometimes moving out of plane, so adding an OnPlane goal to keep them on XY will help a little. Still I can see that having an automatic way of adjusting the sizing to get exact tangency could be useful. I’ll look at adding a new goal for this.
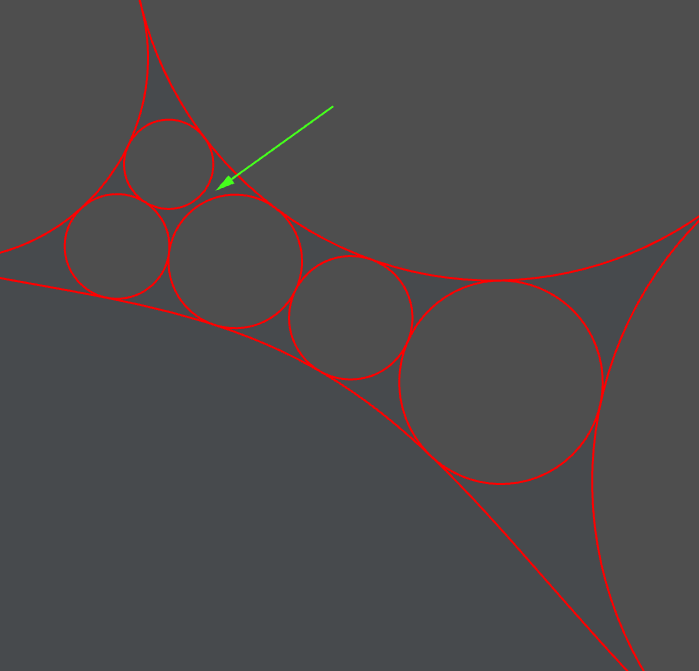
There’s also a new option in the TangentIncircles goal in the latest release to include a boundary curve. These packings do get precise tangency, and it’s a compact circle packing, meaning all the gaps between circles have 3 sides. You can’t explicitly choose the radii with this approach though, since these are uniquely determined for a given connectivity and boundary (up to a Moebius transformation)
it work fine i don’t see any intersection
Here’s a multi-stage approach that does a sphere collision based circle packing first, then gets the connectivity from the Delaunay and optimises that for a true tangency compact packing.
I’ll have a think about an easier way to do this though, and with better control over radii.
Enclosed Boundary Circle Packing2.gh (1.1 MB)
Is it for a phone case?
11 Likes
Wow man, thanks for this. Yes, it is for a phone case. I’m about to go back and set the plane and see what that produces. The whole idea is to get the pack pretty dense within a range of radii. Thanks again for the effort my man!
I added the on plane goal and it seemed to help a lot. Once again my incomplete knowledge of grasshopper was the issue. If there are any intersections, I can’t tell. Now the only thing that would cause clipping would be to add more circles than can be fit into the boundary. Is there a way to “solve” for the perfect circle count?
i dont think that you can get a perfect amount that easy, sooner or later a situation below will happen which would need an adjustment of all the surrounding circles to fit. daniel may cook up something iterative… but that would mean that the entire amount of circles would have to adjust to one perfect equilibrium.
Its not possible to have a circle tangent to more than three circles of different radii. Of course that all depends on the order of circle creation. In the above example I believe the circles were created right to left leaving the gap you pointed out as adding that tangency would result in having to break one of the other three tangencies.
I agree - if the circle radii are prescribed in advance, it won’t generally be possible to achieve a compact circle packing (when all the gaps between the circles are 3 sided).
If you allow >3 sided gaps things are a little easier.
Personally I find true compact circle packings more elegant compared to packings with 4 sided gaps, and they have deep connections to some nice mathematics, such as discrete analytic functions.
1 Like
There’s a nice theorem due to Koebe that says that to every triangulation of the sphere there
corresponds a circle packing, and this packing is unique up to Moebius transformations:
10 Likes
I found I could also use compact circle packings to generate these systems of sliding equilateral triangles:
here showing the underlying circle pattern:
11 Likes
Also, if you generate a pair of circle packings with the same connectivity and different boundaries, it gives you a conformal map between the two shapes:
21 Likes
Hi Daniel,
This might be a trivial question - but how do you ensure/generate same connectivity with different boundaries?
Hi Timothy,
The easiest way is to mesh one shape, then take that mesh and pull its boundary points to the boundary curve of the other shape.
Ah, I see, thanks! I was thinking there was somehow a mapping between the populating (of the vertices) and the edges generation steps. I was perhaps overthinking this but didn’t understand how the pulling of points would always work on more complex base shapes.
It can actually sometimes be useful to pull to a tweened curve, so there isn’t a sudden jump that could cause the mesh to fold over itself.
I want to improve it a bit first, but I’ll post an example like the one above soon.
3 Likes
pulling to a tween curve sounds like a great intermediate step (although i guess tweening has its own issues to begin with) - thanks and looking forward to an example!
Hi Daniel,
is there any .gh definition you can offer yet?