Thanks for the recommendation! I’m currently doing something similar, but I’ve noticed a couple of hiccups that make things much worse.
- Pick a random face weighted by area (this part is done)
- Pick a random point in [0,1]^2 to get UV coordinates
- Evaluate the surface for this point
- Repeat
Here’s an image of what I get with my current setup on a simple object I made with a Boolean Union of two boxes (note that here I don’t include the area weighting as I want to see the effects on the individual faces, instead I just generate 100 points per face):
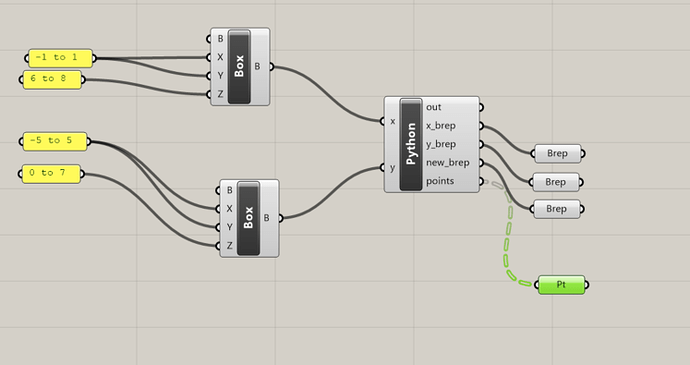
The code in the Python Node:
"""Provides a scripting component.
Inputs:
x: The x script variable
y: The y script variable
Output:
a: The a output variable"""
__author__ = "######"
__version__ = "2022.08.03"
import rhinoscriptsyntax as rs
import scriptcontext as sc
import Rhino.Geometry as rg
import Grasshopper as gh
import Grasshopper.Kernel.Data as ghkd
import clr
import random
import System
# Save old context to reset later
old_doc = sc.doc
sc.doc = ghdoc
# Create Boolean Union of Inputs
x_brep = rs.coercebrep(x)
y_brep = rs.coercebrep(y)
new_brep = rg.Brep.CreateBooleanUnion([x_brep, y_brep], 0.0001)
# Create point samples for each face of the Brep, stored as a DataTree
points = gh.DataTree[rg.Point3d]()
face_counter = 0
for face in new_brep[0].Faces:
face_path = ghkd.GH_Path(face_counter)
face_counter += 1
for i in range(100):
# Evaluate() mutates StrongBox inputs rather than returning the result, so these inputs are created here
new_pt = clr.StrongBox[rg.Point3d]()
new_der = clr.StrongBox[System.Array[rg.Vector3d]]()
# Randomly sample UV coordinates in [0,1]^2
u = random.random()
v = random.random()
# Re-sample UV coordinates if they are outside the Brep Face (give up after 10 tries)
attempts = 0
while not face.IsPointOnFace(u,v) and attempts < 10:
u = random.random()
v = random.random()
attempts += 1
#Evaluate the surface at the chosen UV coordinates
face.Evaluate(u, v, 0, new_pt, new_der)
# Add the surface evaluation to the DataTree
points.Add(new_pt.Value, face_path)
# Reset old context
sc.doc = old_doc
Problem 1: The Evaluate() call does not use a UV parameterization that accounts for the trimmed faces, and so it will potentially generate points on trimmed parts of the faces. This can be seen in the smaller vertical faces at the top of the object in the figures above. Solution: Add an IsPointOnFace() check as stated in OP and scrap points that fail. Note that I set a finite number of attempts to avoid infinite looping, and so the reason the upper faces still generate incorrect points in the figures above is because they max out the number of attempts. The following is a picture of the results with an increased domain size:
Problem 2: UV domain for the faces doesn’t seem to be [0,1]^2 as I would’ve expected; it appears to be in real-world coordinates. As far as I can tell, this will also mess up the mesh approach you describe, as I would assume the UV coordinates of the face mesh will be in [0,1]^2.
I can solve this second problem by baking in some assumptions about the kinds of objects I’m generating (they are all created with Boolean Operations on axis-aligned boxes, so I can simply create a world-aligned bounding box and set the scale of the domain to the size of the bounding box), but I’d like to avoid that if possible so that it is easier for me to use a more general class of objects later.
EDIT: I found the method PointAt() inherited from Surface that avoids me having to use the StrongBox parameters that Evaluate() requires, so I’ve now swapped to that one.