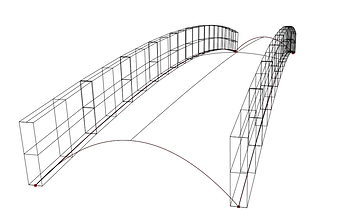
Hello,
I generated a shell structure by using a nurbs surface. And now I would like connect beams and the shell together and then do a mechanical analysis, I did it with a beam which follows the geometry of the side of my shell like this:
But now I would like to add prismatic beams and connect it to the shell, like this:
So I read some karamba topics and I saw some people that the shell and beams can be connected by using Breps and puting inputs points but it didn’t worked. Instead I tried to connect the node of the beam with the nodes of the mesh of my shell by adding some springs between the nodes with a really high rigidity value (around 1e+35 kN/m) but I’m not sure that is really representative of the stress inside my structure. It looked like this:
(Here a view with less visible element of the beam so you can see better how it is connected to shell with the springs)
So instead I want to use the curve used for the generation of my shell. I’m trying to rotate and excentrate the cross section of a beam in order to obtain a straight beam from the curve defined by the curved side of my shell (since I want to connect my beams and my shell for the mechanical analysis). The excentring is working but I still have to rotate the beams sections along the y axis:
I tried to use the orientate element box it is only making rotate along the x axis (in the YZ plane) and since I want it to rotate it along the y axis so I can have my primastic beam I can’t use the orientate element box to have it.
Does someone have any idea how I can rotate my cross section to have my beam straight ?
Thank you in advance for your help and have a nice day.
Killian