Hello, changing provision of control points (degree 6) I see different influence on a surface.
In one case influence comes to an end on thirds to a point, in the second case influence comes to an end on the fourth point. Why so it turns out?



If your curve/surface is single span (cpcount - degree == 1, aka as Bezier) you influence the curve global.
This means, it doesn’t matter which cp you move, you always change the curve as a whole.
Your last image is wrong. The green dot should be at curve end. Its just that you hardly notice a change if 6 controlpoints influence one end, but you could measure influence at any parameter of the curve/surface if you measure curvature numerically (except the end). Rational Bezier/Nurbs can also increase this effect when changing the weight of the cps.
Yes, but and if by sight, on the second picture influence stops on the fourth point. And according to the analysis of Zebra it is visible that on the fifth point influence in fact has stopped (the second image).
I am interested why at different points different force though shift identical up?
if you like to understand how “DeCasteljau” algorithm works have a look at this one:( you can reconstruct a Bezier curve with this manually, without typing in any formula)
Interesting piece.  Thanks!
Thanks!
I recommend the Wikipedia article on Bezier curves for a mathematical treatment and some pretty animations: https://en.wikipedia.org/wiki/Bézier_curve
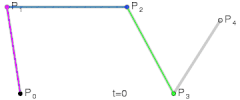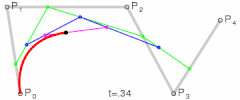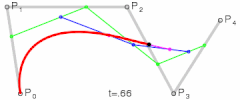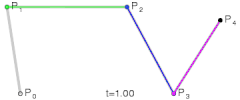
this is actually much easier explained, excluding the nice graphics.
Don’t know what’s wrong with people doing Wikipedia articles about anything related to math 
Ah yes, that looks much better explained with the interactive applets 
(I confess, it was mainly the animations on the Wikipedia page that I was recommending )
no worry, wasn’t meant as critique. The wiki article is still worth looking at, its just that from an engineering or designer standpoint of view, its always overcomplicated, because mathematicians always try to shorten up the information by using symbols all over the place. That’s the same problem expert coders have when writing overcomplicated code, because they know this and that shortcut. Another example:
https://www.rhino3d.com/resources/4560
The NURBS Book
This book covers all aspects of non-uniform rational B-splines necessary to design geometry in a computer-aided environment. Basic B-spline features, curve and surface algorithms, and state-of-the-art geometry tools are all discussed. Detailed code for design algorithms and computational tricks are covered, too, in a lucid, easy-to-understand style, with a minimum of mathematics and using numerous worked examples.
I own this book, but reading this is hard as hell, although it covers everything you need to know.
@qythium, @TomTom, I the same am poor at mathematics, but animation in Wikipedia pleasant ![]()
And article A Primer on Bézier Curves something huge. Somehow I will read.
Here to what it is necessary to pay attention:
The NURBS Book
This book covers all aspects of non-uniform rational B-splines necessary to design geometry in a computer-aided environment. Basic B-spline features, curve and surface algorithms, and state-of-the-art geometry tools are all discussed. Detailed code for design algorithms and computational tricks are covered, too, in a lucid, easy-to-understand style, with a minimum of mathematics and using numerous worked examples.

