Finding "normal" direction at intersection of a polyhedron

[Marcel_de_Lange]

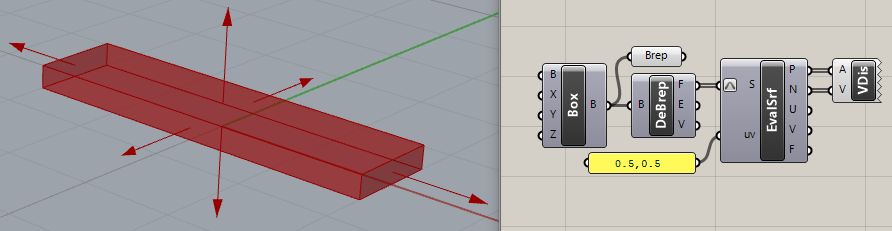
Trying to find best way to calculate the normal direction of the vertex of a polyhedron. I know that when the polyhedron is a full sphere I can use the center and the vertex to get a good estimate. However I cannot figure it out once the polyhedron is for instance trimmed and stretched see image

[Marcel_de_Lange]

I guess I am looking for the average of the 3 or 4 surfaces that connect to each vertex

[Joseph_Oster]

[Marcel_de_Lange]

I am trying to find the “normal” direction at the vertex, based on the surrounding faces, let me know if the below image helps ( the polyhedron is not spherical at this point )

[Joseph_Oster]

@Marcel_de_Lange

let me know if the below image helps

Yes, it’s better than your first image. Even better would be to post the geometry. But there is no normal vector for vertices, only surfaces.

P.S. This might work; expression on ‘V’ input is “-x”.

P.P.S. Here’s a way to avoid the slider using shortest edge length. Expression on ‘R’ input is “x*0.8” (this is so much easier for everyone when you post code/geometry).

[diff-arch]

If you’re dealing with a mesh, instead of a polysurface, you can simply use the DeMesh (Deconstruct Mesh) component, which provides the normals through its N-output.

[Marcel_de_Lange]

I was in the process of adding spheres to the vertices and then take the averages … so this helps a lot Thanks !

[laurent_delrieu]

You can ponderate by face area

or not

[Joseph_Oster]

@Marcel_de_Lange

I was in the process of adding spheres to the vertices and then take the averages …

I’m here to learn and share, how about you?

I just discovered the polyhedron stuff under the ‘Mesh’ tab, so built a test apparatus from it for the code I posted earlier:

I discovered that the method I used works only when the adjacent edges are evenly distributed, but there are solids where that’s not the case and those “normal” vectors look off? What’s the correct way?

brep_vertex_normals_2022Oct16b.gh (32.2 KB)

UPDATE: I discovered that with some shapes it works better to insert a Boundary surface between Polyhedron and Join (Brep Join).
Standby… Rats! Unable to find the example where adding Boundary surface was necessary. Found a few cases though where GH/Rhino hangs!?

[Joseph_Oster]

I vaguely recall installing something related to polyhedra and located this post from three years ago:

Golf ball? Evenly spaced points on a sphere?

I had seen RhinoPolyhedra and just installed IcoSphere but a) these are Rhino commands, not GH(?) and b) no matter what I try, including MeshIcoSphere, I can’t seem to set the number of sides? I don’t know how to get IcoSphere to work at all? I also saw the LunchBox Platonic Icosahedron but it implies 20 sides, fixed, not polyhedron? I squandered more time investigating a C# component I found here, in a model by @laurent_delrieu : It looked promising but the C# code looks sketchy and prod…

Referring to RhinoPolyhedra:

RhinoPolyhedra

And this post in the same thread:

Golf ball? Evenly spaced points on a sphere?

Thanks @dale, I saw that one too and followed the link to RhinoPolyhedra. I thought I had already installed it but to be sure, I downloaded and installed it again. Restarted Rhino. But I’m lost in trying to use it or IcoSphere. [plugins_2019Jul17a] [plugins_2019Jul17a2] [plugins_2019Jul17a3] How do I invoke your plugins? Why is WatermanPolyhedron showing up when I have disabled it? (though as expected, I get this when I use it: “Unknown command: WatermanPolyhedron”) Where do ‘HugelPol…

At the time, I had no luck trying to use it and believe it wasn’t related to Grasshopper. Now I’m wondering if anyone else can see the ‘Mesh | Polyhedra’ tab and run the code in my previous post?

Is this a standard R7 GH feature? Or visible only to me?

[AndersDeleuran]

@Joseph_Oster

Is this a standard R7 GH feature?

I don’t think so. I certainly don’t see it in the latest service release. You can identify the .gha like so:

Plugin bloat victim!

After doing the Ctrl + Alt + Left Mouse Button thing you can also right-click the component on the Component Tabs menu and select Component info: [2019-07-08%2011_25_06-Rhinoceros%206%20Commercial] Which will reveal explicitly the plugin/assembly it comes from: [2019-07-08%2011_25_25-Rhinoceros%206%20Commercial] TreeSloth on this case

[Joseph_Oster]

@AndersDeleuran

I don’t think so. I certainly don’t see it in the latest service release. You can identify the .gha like so:

Thanks very much. I could swear it wasn’t available in Grasshopper when I installed RhinoPolyhedra three years ago. Or maybe I never looked on the ‘Mesh’ tab? It’s a great feature, now that I’ve finally managed to use it in the post above:

Finding "normal" direction at intersection of a polyhedron

I’m here to learn and share, how about you? I just discovered the polyhedron stuff under the ‘Mesh’ tab, so built a test apparatus from it for the code I posted earlier: [brep_vertex_normals_2022Oct16b3] I discovered that the method I used works only when the adjacent edges are evenly distributed, but there are solids where that’s not the case and those “normal” vectors look off? What’s the correct way? [brep_vertex_normals_2022Oct16b2] [brep_vertex_normals_2022Oct16b] brep_vertex_normal…

@dale ?

[dale (Dale Fugier)]

Hi @Joseph_Oster,

Sorry, I haven’t read the entire thread.

Is the question on how to calculate vertex normals? If so, Rhino does so by averaging face normals.

– Dale

[Joseph_Oster]

Thanks, interesting. Averaging the faces adjacent to each vertex? @laurent_delrieu appears to be doing something similar in his post above, but it looks like addition instead of average of face normals?

My question was more about the RhinoPolyhedra plugin being available in Grasshopper. I don’t recall that being the case 3+ years ago?

I’ve just created a GH model that displays ALL the polyhedra by branch in a grid. Very cool to see them. I think my favorite is the “Rhombic Icosahedron” which has 20 equal size diamond shaped faces. It is [index = 15] in category “Other Solids” [index = 17].

The red group is an on/off switch - it takes a couple minutes to run. By the way, as I mentioned yesterday, some shapes require a Boundary surface between Polyhedron and Join (Brep Join). Might indicate a subtle bug?

[dale (Dale Fugier)]

Hi @Joseph_Oster,

@Joseph_Oster

Averaging the faces adjacent to each vertex?

Yes, sorry for the confusion.

@Joseph_Oster

I don’t recall that being the case 3+ years ago?

I don’t recall exactly when GH support was added. But 3 years ago sounds about right.

You can see if you have the latest version using PlugInManager.

@Joseph_Oster

Might indicate a subtle bug?

Not all shapes generate solids. Perhaps this is what you are seeing?

Here is yet another sample:

test_polyhedron2.gh (7.3 KB)

– Dale

[Joseph_Oster]

@dale

Not all shapes generate solids. Perhaps this is what you are seeing?

Not related to solids, no. In the GH file I posted above, in some cases Brep Join turns red with the following error if you skip Boundary and wire Polyhedron ‘C’ (Curves) directly. Adding Boundary prevents that.

[Joseph_Oster]

@laurent_delrieu

You can ponderate by face area

What does “ponderate” mean? Based on Dale’s comment and your second solution, I modified my version ‘16b’ to use the unitized average of adjacent surface normals.

brep_vertex_normals_2022Oct17a.gh (26.7 KB)

[laurent_delrieu]

Ponderate mean that instead of doing the sum of normals and then unitize this sum you multiply each face normal by face area then sum and then unitize.
It is a weighted mean.

First journey in 3D printing

Some weeks ago I began my journey in the 3d printing world. The main job was to generate 3d printer paths from closed curves which represent the intersection between a slice (plane or not) and a solid. The paths must be a single curve, which means the extruder never stop to extrude during the print. The results are very similar from what is presented here and on this paper “Connected Fermat Spirals for Layered Fabrication” The main tool is Offset from Clipper but there are many optimizatio…

[Joseph_Oster]

This might be apropos of nothing, but still interesting?
The white vectors are as before (“the unitized average of adjacent surface normals”), the black vectors (unitized) are obtained from the volume center point and each vertex. For 2 out of 22 vertices they are identical, where 5 faces meet on opposite sides of the polyhedron. For 20 out of 22 vertices they differ, though both look reasonable. All faces have the same area in this case.

brep_vertex_normals_2022Oct17b.gh (25.9 KB)

[revilo239]

Hi Joseph, can you post this definition for download - Please?