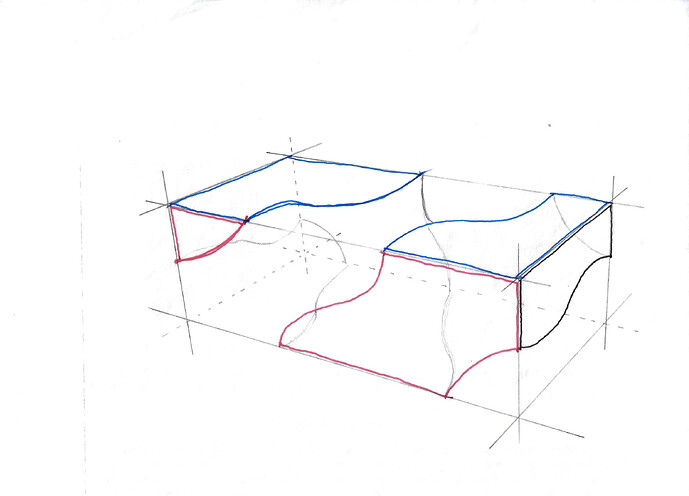
Hello all,
As shown in my sketches (sketches of the same geometry seen from two different orientation), I have been trying to model a solid volume enclosed by a minial surface with a set of boundaries and a bounding box.
I previously tried using millipede with the function defining gyroid
cos(x)sin(y)+cos(y)sin(z)+cos(z)sin(x)=0
Yet this didn’t give me much freedom on controlling the geometry apart from splitting the gyroid with different domain boxes.
My latest attempt is to manually model a discretized portion of a gyroid, which is a method I look up from a paper published on discrete form of the Gyroid after visiting an existing post.
The paper about discrete form of the Gyroid.
Discrete Gyroid Surface
There is also another way I have studied about discretizing gyroid.
Evolution of a Gyroid Surface
I have included both ways of discretizations in the rhino file I uploaded. I have referenced to a script posted on applying Kangaroo mesh relaxation and adjusted slightly to get a smoothed gyroid.
With this approach, the closest geometry that I can get is shown in the pictures below.
I would be very grateful if someone could suggest a way that gives me more control over the minimal surface so that I can achieve the geometry shown in my sketch. Thank you.
Here is the rhino file and Gh definition I used to construct the minimal surface.
gyroid_relaxed.3dm (7.5 MB)
gyroid_relaxed.gh (60.9 KB)