before i start doing binary search maybe somebody has a solution for this. i need a circle with a constraint center line, that means the center can be anywhere along this yellow line but to its maximum size regarding the corner below where it hits the boundary. the upper line is 99. something percent straight so rather negligible. the cirlce seen here is a crude approximation and was done by using the upper end and the line itself as a directional constraint… but like that i cant use any smarttrack tricks which help me connect at a local maximum. any ideas? i already tried all cirlcle tools with all circle tangents. but nothing stays in the center line and geometric translation also does not work due to the dynamic dimension of the circle.
well i solved it with 0.0025 mm off the boundary, thats good enough for now so no urge on this. if somebody still wants to scratch up a 100% solution i would be glad to listen. but i believe it would imply something like grasshopper or a scripted algorithm maybe. @Helvetosaur any thoughts? growing/scaling a circle along a line till it intersects with a curve?
hi Simon, yes tried that, it works ok but its not 100% precise.
it creates a areacentroid which is 0.05 mm next to the line where it should be.
its sure not much but not very assuring. i constructed it geometrically in the end
and got a much higher precision still not exact as i would say,
but anything with circles is always a bit hazy probably…

I do not see this difference. The center of the circle (with the settings in millimeters) I know match the vertical line. The difference between the point of the center and the line is 0:00 mm
maybe thats because you rebuilt it and used a straight line on top, mine is not 100% straight. here a cut out file of it, just select the point and use ZoomSelected or scroll into the point till you find the prepared line
CirclewithConstraints.3dm (2.6 MB)
you can even see when zooming in into the last tangent while constructing the circle that its off.

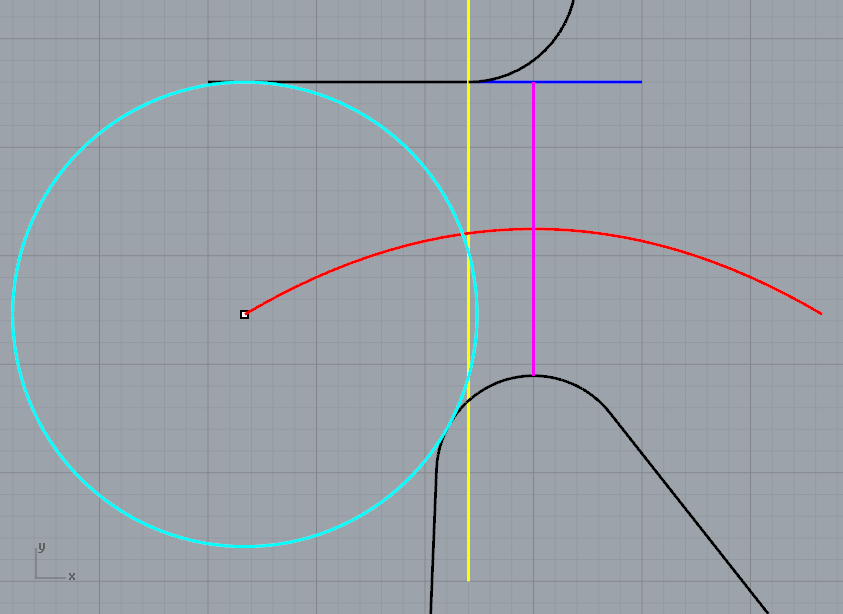
How about constructing it geometrically like this?
-Find the (magenta) line perpendicular to both the (extended) straight line (blue) at the top and the arc at the bottom
-Make a circle (cyan) tangent to both the top and bottom curves
-Make a parabola(red) by vertex and direction. Using the midpoint of the magenta line as the vertex, its direction, and the circle centre as the end point.
-The centre of the circle you are after must lie on this parabola, where it intersects your vertical line.
its a very interesting solution. the yellow one is your Areacentroid, while the green one is from my messings and the blue point is the rhino onboard solution with 3 tangents and 0.05 mm off which also Simon suggested which is unfortunately the least precise.

i had trouble constructing your suggestion at first since i never used parabola, so with a few fail attempts but following your exact description i managed. just my geometric-iterative solution gave me 2 intersection with the arc below and your solution has none but being only 0.0023 mm away from it. so both are not 100%

@DanielPiker maybe its because your method would work only when the upper line is straight? but since its slightly curved it would maybe need something like 2 parabola… but for me your solution is already completely alien and i would have never thought of that… but still no real solution afaics at least not if you really need it exact.
@RichardZ - Yes, the method I posted will only work when the line is straight (and when it is it should be exact).
I can see how it seems an odd approach at first, but I think of it like this - for a circle to be tangent to 2 curves, the distances from the circle centre to the closest point on each curve must be equal. Therefore the centre lies somewhere on the curve which is midway between the 2 curves. I remembered from Fortune’s algorithm for calculating Voronoi diagrams that this midway curve for a point and a line is a parabola (and this is true also for a circle and a line, or for 2 circles).
It might be possible to adjust this approach to work when the top curve is an arc instead of a straight line.
Also, if you don’t mind using Grasshopper/Kangaroo, here is a way of solving this numerically that will work with arbitrary curves.
tangent_to_curves.gh (9.2 KB)

Hi Daniel, thats superb more than i could´ve wished for and certainly kicks it into the right direction. i assumed that this might end with something numeric and you delivered a solution which also will work on any kind of curve and not just arcs. thanks a bunch, now i have something to learn from for getting back into Hopper/Roo
still interesting though how your geometric solution might work in case of having two arcs one on top and one below which would imply using your parabola method but with two fokus points influencing a middle line something to think about maybe.