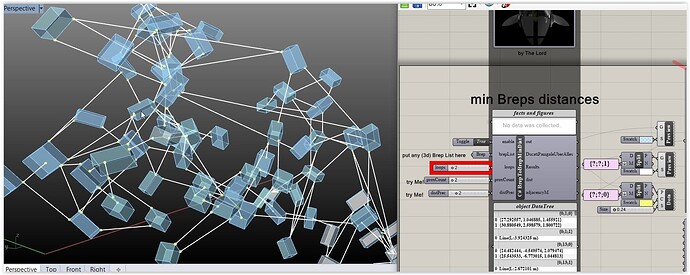
This is an iterative procedure to find the closest point on both BReps. First you start with a point on one BRep A, then from that find the closest point on BRep B. Then using the closest point from B, find the closest point on A, etc. etc. until there are no more changes.
Can you demonstrate it with a chart? I’m a bit confused
I’m here to study this issue again
If one of the two objects is a sphere, it’s simple.
Why is it like this? There are two situations now: a sphere and a cube
The closest point between a sphere and another object can be found by getting the closest point from the center of the sphere and the object first.
Then create a line between the center and the point on the other object and get the intersection.
I have roughly understood a bit. What about a cuboid? How can I determine if Brep is a circle or a cuboid
Circle or cuboid….
You mean sphere or cuboid?
How to determine whether Brep is a sphere or a rectangle
A sphere or a box you mean ?
None of the two objects can be a rectangle cause that’s not a brep.

These are the two Breps
Received, will try to write a Python program
This method reports an error when identifying non spherical objects
This idea is very good, but when it comes to writing Python, I’m a bit clueless
Try to get the gist of the logic (that’s C#) and then … try to write something similar in P.
Explanation: this works with Lists (of any Topology - shown boxes for clarity).
- Get a pair of Breps (say b1, b2) that are not taken (using a bool [ breps.Count , breps.Count ]).
- Define a rnd pt in b1.
- Find the closest pt in b2.
- Define one from the other and the other from the one. See Loop with 2 lines: pt1 from pt2 and then pt2 from pt1.
- In real-life one needs 4-6 iterations (contolled by the loops val).
Tip: as an option [case: “heavily” concave Topologies - you can inquire these via various ways] you can apply 2 passes: first approximate using solely Boxes and then refine using Breps (or Meshes or cats or dogs or whatever).
Tip: as a PlanB you can define pts on b1, b2 Faces (i.e. not inside) and find the closest pair (via a classic divide and conquer approach and the likes).
PS: That way you can do some sort of a “Graph”, locate Islands (*) and do an A-Star Routing where nodes are Breps/Meshes/Whatever (instead of classic points).
(*) Islands means a 2 dim BrepBrep Connectivity Tree where 1st dim is the Cluster index.
Here’s a small iterative function I once wrote that might help:
231019_BrepsClosestPoints_00.gh (122.8 KB)