Hi everyone,
I usually try to ask questions regarding knowledge about grasshopper. This time I thought I might ask some help in solving a geometric question.
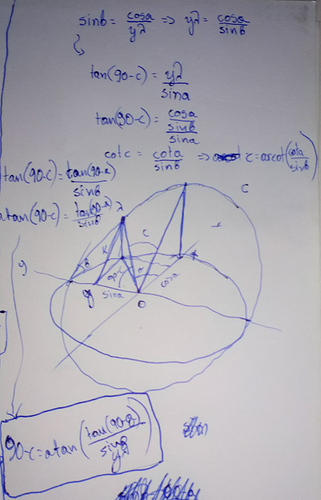
I am trying to calculate trigonometrically the projected arc from a circle in the xy plane to another plane with an angle to it. It’s been a long day and my mind is jammed so if anyone is interested and would like to have a look at it I would appreciate it.
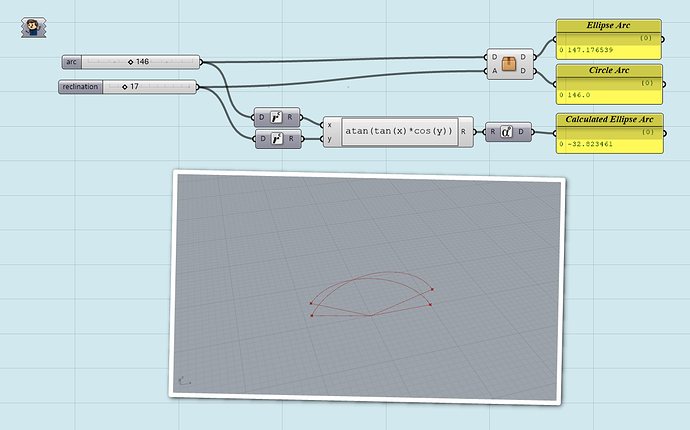
arcEllipse.gh (18.7 KB)
Is the angle of the gap all you need before and after projection?
No, the opposite, I noticed it now.
It should start from x and measure counter clockwise from 0 to 360.
the vector angle always choses the smallest of the two arcs. we don’t want that
Now I genuinely don’t know if it is a GH thing or a geometry thing.
the expression that I came to is atan(tan(x)*cos(y))
(no cotans btw  )
)
It should work for all quarters, but for some reason it jumps back and forth between 0 and 90…
I even tried using absolute values for sines and cosines but still no good.
arcEllipse.gh (16.7 KB)
You need to specify a plane (likely the XY plane) in order to get the full 0 to 2pi (360) angle in your top “angle” component. I don’t know how to fix your exact issue of your numbers not agreeing but I do know that in order to get your full angle you need a plane.
hi andy,
you are right but what you say applies to the ‘mechanical’ way of finding the angle.
My concern is primarily the trigonometric formula.
Trig it is… GH doesn’t like giving the negative but it’s ultimately the same. Modulus forever!
ArcAngle.gh (12.4 KB)
And if you don’t want the reflex angle you can always do ( 2*pi - yourangle)
If it’s vectors in 3D space, vector arithmetic is usually a lot more elegant than trigonometry. But that would involve you inputting the planes into the expression as well.