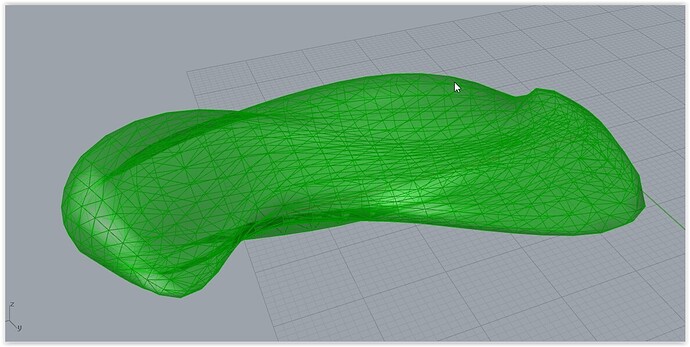
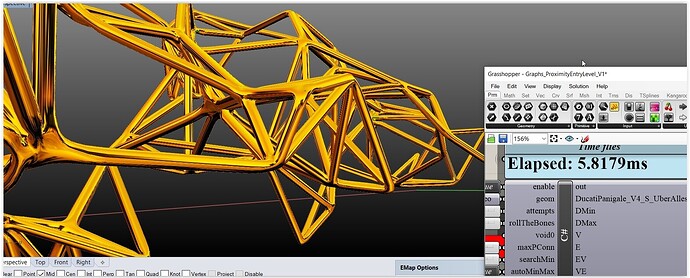
Hy everyone,
I need to adjust the points of the structure in the figure so that the edges are not higher than 45 ° with respect to the XY plane. It doesn’t matter if the structure changes geometry considerably, but for molding reasons I have this need. In recent days I have received some answers on this, but I would like to know with which function it is possible to do a similar operation.
In case I can share 'design algorithm. Thank you.
Doable via components but these are not my game. So get a C# that does it (by rotating the lines found outside the desired aMax value).
Lines_RotateToMaxAngleToPlane_V1.gh (9.7 KB)
Thank you for the suggestion.
But actually I would prefer to orient the points with respect to an XY plane.
And also with this function how do I establish the angle evaluation reference?
OK, that C# was a naive entry-level stuff (meaning that a lot of cases/options are excluded). I’ll provide the real-thing later on.
Thanks but that doesn’t change much (for the general case, that is: given any collection of lines AND any user defined plane … do the rotation as you want).
But indeed I need some moral help related with Valentino and this w/e MotoGP.
Well … the attached (as also the previous one) rotates lines. Lines define directions and thus the rotation VS some test max angle has some meaning by measuring the angle between 2 vectors (the direction and the “projection” of that vector in a given user defined plane) with respect a “rotation” plane, That said the angle between a point and a plane … er … has no meaning.
This means that is your responsibility to indicate/locate/find the lines (where the end or the start contain the point of interest).
For instance in a given 3d graph get the naked nodes - i.e. nodes with valence 1 (use classic vv connectivity trees) etc etc.
Lines_RotateToMaxAngleToPlane_V1B.gh (150.8 KB)
UPDATE:
Well … you are using Voronoi (I hate that thing) for your graph. That’s 100% Academic and totally unsuitable for any kind of rational engineering (even for artistic purposes), See a proximity take on that matter. You can get your prox pts collection using a Brep or Mesh as container as well resulting a far more interesting - i.e. not something out of an ugly box - graph (notify if you need a C# demo) and a distorted 3d grid that “looks” like random points in 3d space - meaning 100++ times faster results.
Added a simple C# that - if enabled - can guide you for picking realistic R+/R- prox values.
The only issue with the proximity is that it MAY yield islands. Island detection is done solely via the VV connectivity tree (but my C# that does that is strictly internal).
Lines_RotateToMaxAngleToPlane_V1C.gh (134.6 KB)
Thank you very much, there is no other way to evaluate the angle of the edges generated by the voronoi structure so as not to vary the structure too much. It would be very useful for me.
To sum up:
- If I was you … I would completely abandon Voronoi for doing any rational 3d graph (and then thicken it into some Mesh via stuff the likes of ExoW (avoid), IntraLattice (ditto) or Dendro (hmm)).
- I could provide a C# that does a random prox graph in real-time ( plus the EV, VV classic connectivity Trees - MINUS the island detection part) using as a container any valid closed Mesh or solid Brep (including obviously a Box).
- That graph MAY or MAY not have naked edges.
- If your issue is the “stability” of the naked ones (as shown in the V1C) AND If there’s naked around … then you can rotate them up to some desired max angle (with respect a given user defined plane).
So if you want a C# on that matter, notify.
PS: Given a graph are you fully OK with what connectivity means ?
Can you show me how you plan to generate a similar structure by not using the Voronoi structure.
Because, at the moment, no solution has been provided for what I requested. Thanks.
As I said the proximity way (briefly outlined in V1C) could use a container (general case) and random points inside. Then it computes the connections with respect min/max distances and the max connections allowed.
Illustrated the procedure has as follows (in action a C# that works differently than the native prox component - since, in my case, that kind of stuff is solely used for random trusses and the likes - I’m in the AEC market sector).:
Note: The “shape” of the graph is more or less dictated by the container and the density of the points. There’s various ways to control the creation of the naked edges but none of them is suitable for a novice not familiar with code. The last pics are TSpline tubes (questionable quality results [twists], mind).
Note: As you can see the big thing with proximity is the island detection … and in 99.99% of cases the structural integrity of the graph (if you want to use it as a truss). But with regard the structural part the Voronoi approach is way worse (and it takes ages to finish and it may yield tiny segments and …).
Note: The V1C does a prox graph using a box.
Anyway If you want that C# notify (but if you are not familiar with code … there’s not much that can teach you).
So I could generate any geometry (box type) and nest random points inside to get a shape similar to the one I wanted. So is it easier to adjust the edges of the structure?
Given any Graph is very simple to locate the naked edges (as shown in V1C) … but for that you’ll need to FULLY understand what a VV (V for vertex) connectivity is and how to use it (elementary via code but also doable via components). For Graph read a given island in a given Graph (if islands are around).
That said connectivity is a DataTree (of type integer) that correlates one or two Lists (by index). The last path dimension per branch is the index of the item in the first List and the items in the branch are the indices of the items in the first (or second) List. The VV connectivity correlates vertices to vertices (what is connected to what) thus using a single List.
But if your goal is to do an AEC thingy (with load bearing capabilities) the naked edges are just ONE part of a big challenge. Just think that a “stiff” Graph is one where tetrahedrons are involved (per a quad set of vertices): the more you deviate from that topology … the more flexible the Graph is. With this in mind a Voronoi 3d thingy is just the total distaster.
Thus it does not appear to be a form of triangularization of the system, in which each vertex carries with it the various indices of the sides.
Can you let me have some examples so I can study the model.
Well … get this … but is 100% C# AND is restricted (all things that have some meaning in real-life AEC matters are removed [islands and some other stuff]). Works with any valid GeometryBase input that is either a closed Mesh or a solid Brep.
Graphs_ProximityEntryLevel_Public_V1.gh (158.3 KB)
Unless you have plans to learn how to code is not that usefull for you (but in the V1C provided above there’s native components around).
The important part is the way that you access the vertices/edges and their neighbors (vertices or edges): The thing provides a List of vertices (V) and edges (E) and the 3 common connectivity DataTrees that we are using in Graphs (in fact in real-life V and E are one dimension paths Trees and the conn Trees have 2 dimension paths - where the first is the island index). So it differs from the prox component. Plus it measures the min (of mins) and max (of mins) distances and restricts the search (auto mode) within that Domain of values. Is written having solely real-life big AEC trusses in mind (where triangulation [and stiffness] is king).